職 稱:退休榮譽講座教授
E-mail:yjlee@nuk.edu.tw;yuhjialee@gmail.com
最高學歷:美國紐約州立大學(水牛城分校)數學博士
專 長:機率、泛函分析、微分方程
研究簡介:
- 1979~1985年間主要從事無限維空間上的微積分與Path integral的研究,這方面的研究始於由L. Gross所建立的abstract Wiener space與其後續的Potential Theory on Hilbert space,其工作引響所及除了無窮變數函數的微分(Gross的H-differentiation)與積分(Path integral)及基本理論訊速發展外,無窮變數的維分方程的研究也狂熱的被重視,這段時間我的工作主要是研究高階無窮變數微分方程的解的存在性、唯一性與正則性。主要貢獻是引入Fourier-Wiener變換的方法。
- 1985-1998年間開始從事無窮維廣義函數論的研究,也就是白噪音分析(white noise analysis)又稱為Hida Calculus,由T. Hida在1975年首創,該理論己被廣泛地應用在許多領域,如量子機率論、量子場論、隨機分析、隨機微分方程等。我的研究主要是引進Schartz的方法重新建構Hida Calculus及其應運用,我的方法與Hida的不同可由以下white noise
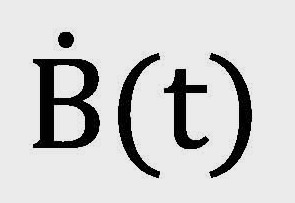 的定義看出來:
的定義看出來:
- Hida定義
 其中S-1為S變換的反變換,當
其中S-1為S變換的反變換,當 為試函數時
為試函數時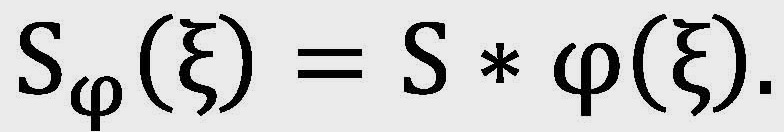
- 本人則定義
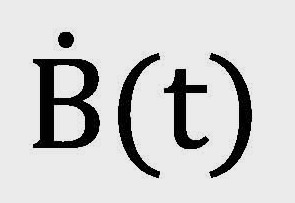 為以下線性泛函:
為以下線性泛函: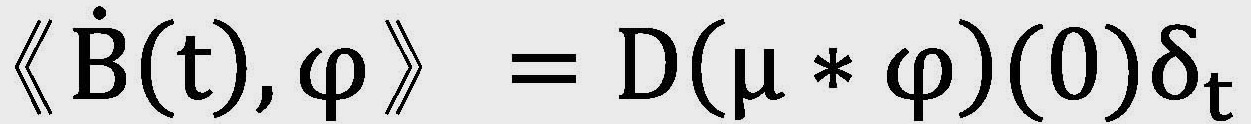
其中µ表無限維空間上的Gauss測度。
重要貢獻有
(a) 證明無限維空間的Hida試泛涵(test functionals)具有解析修正(analytic version)。此成果為無限維空間的Hida Calculus的
基本結果之一,並使Hida Calculus的研究基礎得以建立。
(b) 推廣Riesz表現定理與Weierstrass定理至無窮維空間。
(c) 推廣Heisenberg Uncertainty至無窮維空間。
3. 1999年開始研究Non-Gaussian white noise analysis,這方面的研究主要與本系施信宏教授合作,詳情請見施教授研究工作說明。

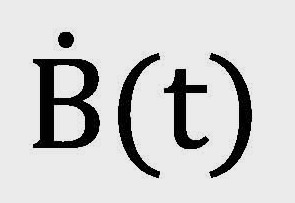 的定義看出來:
的定義看出來: 其中S-1為S變換的反變換,當
其中S-1為S變換的反變換,當 為試函數時
為試函數時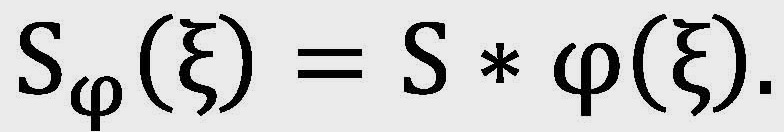
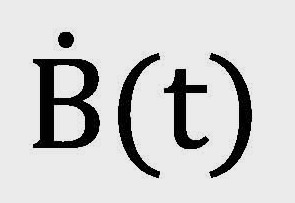 為以下線性泛函:
為以下線性泛函: