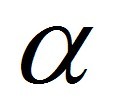教師姓名

自從日本數學家 T. Hida 在 1975 年發表高斯型無窮維廣義函數論，也就是白噪音分析 (white noise analysis) ，他的理論已被廣泛地應用在許多領域，如量子機率論、量子場論、隨機分析、隨機微分方程等。

我的研究主要是推廣Hida的架構至 (1) 一般性的Levy過程或是 (2) 古典的溫式空間(classical Wiener space)，建立適當的廣義函數理論，然後在此架構下解釋其相關的隨機現象。研究工作大致分成以下兩個部分：(A) 針對滿足動差條件的Levy過程，發展出一套Levy白噪音calculus。例如，導出Segal-Bargmann變換之closed form；透過Segal-Bargmann變換研究Levy泛函的微分算子及其對偶算子；定義廣義多重Levy隨機積分和Levy過程之Donsker δ-函數；推導廣義Levy泛函之It\^o公式；導出不可預期Levy泛函之Kubo-Takenaka公式；以及研究Levy過程的Hitsuda-Skorohod積分。(B) 將(A)的結果更進一步地推廣至無動差條件的Levy過程，尤其是具特徵指標 (0< <2)的穩定過程( -stable process)；連接Levy白噪音分析和量子機率論，例如，建立 Levy白噪音的量子分解定理；廣義Levy泛函之Clark-Ocone公式的研究；以及推廣Stein方法至無窮變量常態逼近(infinite-variate normal approximation)。

My current research interests are in the areas of mathematical biology and medicine including problems concerning the hormone interactions of the endocrine system, tumour modelling and cell signalling. My previous work involves problems with applications to solid mechanics. Currently I am combining the two areas of work employing solid mechanics in the modelling of tumour growth. I use ODEs and PDEs (continuum models) in my modelling and employ singular perturbation technique to simply the analysis. For the most recent project concerning the hormone interactions within the endocrine system, we constructed a model of delayed differential equations that describes interactions and feedback of hormones along the hypothalamuspituitary-ovary axis and exploited the nature of multiple timescales resulting in a simplified
system of three delayed differential equations. The relative simplicity enables a more detailed analysis of the solution structure in large time while at the same time is capable of reproducing the myriad of the solutions exhibited by the more complicated models. The predicted hormone concentration is currently being incorporated into the modelling of myoma growth. As well as considering the influence of growth-induced stress on tumour expansion, we are interested in the effect of hormone on tumour development, particular when such effect is induced by externally applied drug treatments. I have also worked on problems in the area of solid mechanics, in particular fracture mechanics using singular perturbation technique and have modelled problems that describe flow efficiency into the wellbore with applications to the oil industry. Recently, I have collaborated with my colleagues studying the multiplicity of solutions to some Dirichlet boundary value problems.

目前研究方向為組合數學。主要的研究內容是討論滿足一定條件下的組合結構的建構、計數及 q-類比的相關問題。例如：古典類型的不相交劃分、m-可除的不相交劃分、pattern avoidance 等相關問題的研究。

另外，對組合設計理論及編碼理論相關問題亦有興趣。

主要研究領域是離散數學及其應用，近幾年特別著重群試設計(group testing)的研究，以下為群試設計的簡介：

從1942年至今，群試設計相關的研究不斷地發展及演變；傳統群試問題是要從含有正克隆(positive clones)及負克隆(negative clones)的群體中識別出正的克隆，其所使用的工具是群試驗(group tests)，如何減少群試驗的使用量是主要被討論的問題。從初始的血液測試到後來在計算分子生物及通訊網路上的應用，不斷有各類的群試模型被提出；我們研究有仰制物群試模型(inhibitor model)、複合物群試模型(complex model)、門檻式群試模型(threshold model)、多數決群試模型(majority group testing)、圖限制之群試模型(group testing with graph-constraint)等等。逐步演算法(sequential algorithm)及非調整型演算法(nonadaptive algorithm)是兩大群試演算法類型；前者採取逐一進行的試驗，每個試驗可依據先前試驗結果而設計；後者是依據模型的訊息及假設而設計同步進行的試驗。當然也有其它類型的演算法。

以下列幾個研究群試設計可能採用的工具及其相關領域以供參考：組合方法、圖論、機率方法、編碼理論、演算法、代數、線性代數等等。

在2006~2011年期間，本人從事調和分析領域的工作，主要工作著重於各種奇異積分算子在加權Lebesgue空間及加權Hardy空間上的有界性。這個主題是由Calderon和Zygmund在1950年代引進，所以常被稱為Calderon-Zygmund奇異積分算子。這類算子之所以重要，一方面是因為它是Hilbert與Riesz變換的推廣，而另一方面它與偏微分方程和擬微分算子皆有相當密切的關連。研究算子在某一空間上的有界性，常常也牽涉到此一空間的性質，因此我們也對Hardy空間做了一番瞭解。

自2012年起，本人開始著手於偏微分方程方面的工作，主要考慮流體力學與非線性平衡律相關方程，例如：交通流、管道流、多孔介質二相流與淺水波方程等，研究著重於解的存在性、唯一性和穩定性與解的各種行為特性。

生活中許多物理現象及生物系統相關的問題，都能用數學加以解釋，甚或能用好的數學模型來預測整個系統的動態。我的研究興趣主要集中於流體界面問題的數學建模、科學計算、以及偏微分方程數值方法；在數學上，這些界面流問題，可以藉由Navier-Stokes方程以及物理法則所推導出的邊界條件來描述，基於整個數學模型的複雜度與解析解的困難度，數值方法的求解是必然的。有表面活性劑的界面問題，在化工、生物學、生理學及物理學中扮演很重要的角色，相關例子包含化妝品的製造、藥物制作(嬰兒呼吸窘迫綜合徵)、以及清潔劑和洗衣精的合成等。過去幾年，我發展了一個能處理有表面活性劑界面問題的數值方法(A conservative numerical scheme for surfactant concentration equations)，藉以研究活性劑如何改變表面張力，而影響整個系統的動態及穩定態。我近期的研究工作則是界面在zero-vorticity附近的局部穩定性分析，以及用數值模擬作相關參數的研究；而這項研究主要啟發於解決石油洩漏對墨西哥灣海洋生態的破壞。另一項近期的工作著重於研究細胞膜性能（如表面張力、附著性、彎曲剛性）對吞噬作用(endocytosis)的影響。(Endocytosis是細胞生物學中的重要功能之一，主要工作為內化分子、蛋白質、顆粒等進入宿主以維持細胞穩態。)

我的研究主題為符號動態系統與遍歷論，一旦給定的函數行為具有馬可夫分割時，即可透過符號系統來研究其結構，如：混沌性、碎形維度等等。即便不具有馬可夫分割，在滿足某些特定的條件下，我們還是可以透過符號系統來研究其自身行為，目前的研究主力為數論中的beta transformation以及由無窮tree所產生的符號系統。

在此同時，我也將這些理論應用在多層神經網絡以及細胞自動機的研究。一維的多層神經網絡以及細胞自動機的性質已有不少結果，現正進行中的幾個議題為：減少神經網絡層數的充要條件，發展神經網絡反問題的演算法，限制在特定子空間的自動機動態行為，以及二維上的討論。

在矩陣理論及計算的研究領域中，主要是研究『特徵值問題』，其中包括非負矩陣及M矩陣。這些矩陣主要來自於各種應用問題，其中包括隨機過程、網頁彼此之間的超連結關係、有限元素法或有限差分法。由於在應用上(例如:影像處理)，需要處理大型稀疏非負矩陣或者M矩陣的特徵值，這其中牽涉到最大特徵值或最小特徵值的存在唯一性。因此，在理論方面我主要研究最大特徵值與其向量的存在唯一性；在計算部分，主要發展高效能的演算法。

　　目前的研究為:張量(tensor)計算領域中的『張量特徵值問題』。在這邊的張量主要是指高維數據的一種表示，亦可以看成矩陣的推廣。在數據科學(data science)中，對數據或大數據(big data)的表示主要有圖模型與張量(tensor)兩大類方法。隨著傳感器(sensor) 技術和存儲(storage)技術的進步，所獲得的資訊非常龐大，而且這些數據彼此之間並不是互相獨立的，往往具有一些錯綜複雜的關係，這類複雜的關係通常能以超圖結構(hypergraph)和張量(tensor)的形式來表示。張量表示的優點在於並不會破壞原始數據的局部和全局結構，能最大限度地保持原始數據的固有信息。