職　　稱：教授

辦 公  室：理學院430室

電　　話：07-5919168

傳　　真：07-5919344

E-mail：hhshih@nuk.edu.tw

最高學歷：國立成功大學應用數學所博士

專　　長：白噪音分析、Levy白噪音分析、隨機分析

個人網頁

研究簡介：

　　自從日本數學家 T. Hida 在 1975 年發表高斯型無窮維廣義函數論，也就是白噪音分析 (white noise analysis) ，他的理論已被廣泛地應用在許多領域，如量子機率論、量子場論、隨機分析、隨機微分方程等。

　　我的研究主要是推廣Hida的架構至 (1) 一般性的Levy過程或是 (2) 古典的溫式空間(classical Wiener space)，建立適當的廣義函數理論，然後在此架構下解釋其相關的隨機現象。研究工作大致分成以下兩個部分：(A) 針對滿足動差條件的Levy過程，發展出一套Levy白噪音calculus。例如，導出Segal-Bargmann變換之closed form；透過Segal-Bargmann變換研究Levy泛函的微分算子及其對偶算子；定義廣義多重Levy隨機積分和Levy過程之Donsker δ-函數；推導廣義Levy泛函之It\^o公式；導出不可預期Levy泛函之Kubo-Takenaka公式；以及研究Levy過程的Hitsuda-Skorohod積分。(B) 將(A)的結果更進一步地推廣至無動差條件的Levy過程，尤其是具特徵指標 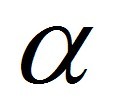(0< 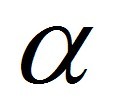<2)的穩定過程( 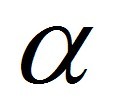-stable process)；連接Levy白噪音分析和量子機率論，例如，建立 Levy白噪音的量子分解定理；廣義Levy泛函之Clark-Ocone公式的研究；以及推廣Stein方法至無窮變量常態逼近(infinite-variate normal approximation)。